Factor de potencia y coseno de fi: las tres dimensiones de la corriente eficaz

Los que peinamos algunas canas o incluso son más jóvenes, hemos crecido tratando al factor de potencia y al coseno de fi (cos φ) como sinónimos. Hoy que nos vamos habituando paulatinamente a las fuertes distorsiones en las corrientes de carga de los sistemas eléctricos y sus efectos sobre nuestras instalaciones y equipamientos, es necesario poner un fuerte énfasis en las importantes diferencias que existen entre estos dos conceptos que, lejos de ser sinónimos, provienen de definiciones muy dispares.
Para el estudio de ondas periódicas deformadas (no senoidales) se emplea la serie de Fourier, que descompone la onda en cuestión en una suma infinita de ondas senoidales perfectas cuyas frecuencias son múltiplos enteros de la frecuencia fundamental de la onda. El componente senoidal de la misma frecuencia que la frecuencia de la onda analizada se llama justamente “onda fundamental”, “componente fundamental” o “armónica fundamental”. Los demás componentes se identifican por su “orden”, un número que indica cuántas veces mayor es la frecuencia de ese componente respecto del fundamental. Por ejemplo, una armónica de orden 5, también llamada “quinta armónica”, tendrá una frecuencia de 250 Hz en un sistema donde la frecuencia fundamental es de 50. Este método se trata ampliamente en la electrotécnica, y para este artículo se requiere estar familiarizado, aunque sea ligeramente, con sus conceptos.

Empecemos por definir el factor de potencia (FP). El propio término nos remite a su definición: es el factor que relaciona dos potencias:

FP = Potencia activa/Potencia aparente = P/S

Recordemos que por “potencia activa”, también llamada “potencia real” o “watada”, nos referimos a potencia mecánica o calor, expresada en watts o sus múltiplos más comunes: kilowatts o megawatts. Potencia aparente en un sistema eléctrico es el producto de la tensión por la corriente:

S = U . I

Y para diferenciarnos de la potencia activa, la potencia aparente se expresa en volts por amperes, o voltamperes y sus múltiplos kilovoltamperes o megavoltamperes. En la ecuación, los valores de tensión y corriente corresponden a sus verdaderos valores eficaces (TRMS, por sus siglas en inglés) totales.
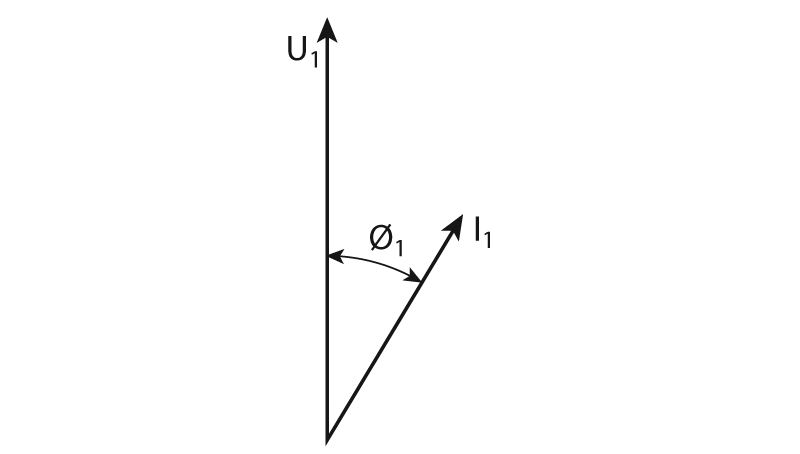
Volviendo a la definición de “potencia activa”, esta solo se logra cuando los vectores de la tensión y la corriente están en reposo relativo entre ellas. En corriente alterna, esto significa que están girando a la misma velocidad ambos vectores, o sea, que tienen la misma. Esto ocurre, en particular, para la frecuencia fundamental. Por esta razón matemáticamente involucramos los valores eficaces del componente fundamental tanto de corriente como tensión y el coseno del ángulo que esos vectores forma, llamado fi (cos φ).

P = U₁ . I₁ . cos φ₁

Aquí los subíndices indican que nos referimos al valor eficaz de la primera armónica, o sea, la de frecuencia nominal u onda fundamental. En el caso ideal de tener una distorsión nula, tanto en la forma de onda de tensión como de corriente (THDi = THDu = 0), significa tener formas de onda perfectamente sinusoidales, y solamente en esta situación valen las igualdades siguientes:

U₁ = U

I₁ = I

Los verdaderos valores eficaces de las ondas fundamentales son iguales a los verdaderos valores eficaces totales de tensión y corrientes cuando no hay distorsión. De cumplirse esta condición, podemos reemplazar en la ecuación de la potencia aparente:

S = U₁ . I₁

Si volvemos ahora a la definición de factor de potencia y reemplazamos estas últimas expresiones:

FP = (U₁ . I₁ .cos φ₁ )/(U₁ . I₁ ) = cos φ₁

vemos la razón de nuestra interpretación histórica, es decir, la igualdad entre el factor de potencia y el coseno de fi. Pero no debemos olvidar que para llegar a esta igualdad, tuvimos que suponer que corrientes y tensiones son senoidales puras. Esta situación, que era frecuente encontrar en los sistemas eléctricos industriales y domiciliarios hasta hace unos cuarenta años, es hoy en día más una excepción que la regla. Dispositivos electrónicos como televisores, PC, hornos de microondas, lámparas de bajo consumo, motores alimentados mediante variadores de velocidad, hornos de fundición, máquinas de soldar thiristorizadas y otros dispositivos, tanto de consumo masivo como industriales, tienen corrientes de carga que distan muchísimo de tener formas de onda senoidales. Para todos estos ejemplos, la última ecuación es totalmente inexacta y en la generalidad de los casos debemos expresar que:

FP ≠ cos φ

Veamos de graficar un poco mejor dónde está la diferencia y cómo introducir las nuevas condiciones de carga en nuestro análisis histórico de corrientes, tensiones y potencias. Para estudiar el comportamiento de las corrientes y tensiones no senoidales, se analiza cada armónica por separado, siendo esto relativamente sencillo ya que son ondas senoidales puras cuya electrotecnia manejamos con familiaridad. Luego, sumamos todos los resultados obtenidos y nos dará el efecto buscado, producto de la onda distorsionada. Este método se conoce como “superposición”. El verdadero valor eficaz de una corriente o tensión distorsionada es el promedio de la suma cuadrática (de ahí las siglas TRMS) del valor eficaz de cada armónica.

I = √(I₁² + I₂² + I₃² + I₄² + I₅² + ... I_n²)

U = √(U₁² + U₂² + U₃² + U₄² + U₅² +... U_n²)

Jugando un poco con las últimas ecuaciones, podemos introducir un concepto nuevo. Vamos a llamar verdadero valor eficaz de la distorsión a la siguiente expresión:

I_D = √(I₂² + I₃² + I₄² + I₅² +... I_n²)

U_D = √(U₁² + U₂² + U₃² + U₄² + U₅² +... U_n²)

Notamos que aquí tenemos el valor eficaz de todas las armónicas menos la fundamental. Este valor nos dará una idea de la magnitud de distorsión de nuestra tensión o corriente.
Analizando lo último que expresamos, podemos escribir la expresión de verdadero valor eficaz total:

I = √(I₁² + I_D²)

U = √(U₁² + U_D²)

Acabamos de ver expresada de manera sencilla y entendible la influencia de la distorsión en la magnitud de los verdaderos valores eficaces de la tensión y corriente. En general, es muy frecuente encontrar en las instalaciones de potencia fuertes distorsiones en la forma de onda de corriente y distorsiones mucho más leves en la forma de onda de tensión. Esto se debe a que la forma de onda de tensión es provista por la red y los sistemas empleados son de tensión constante, mientras que las corrientes son demandadas por los usuarios, y los dispositivos toman de la red corrientes de manera caprichosa o controlada, produciendo formas de onda no senoidales. Vamos a suponer, para no complicar demasiado el análisis en este artículo, que la tensión permanece aproximadamente limpia: U ≈ U1. Ahora vamos a descomponer el vector fundamental de corriente de la última expresión en sus componentes activa y reactiva:

I₁ = √(I_r1² + I_x1²)

Introduciendo esto en la ecuación general anterior donde contemplamos la corriente de distorsión nos queda la siguiente expresión:

I = √(I_r1² + I_x1² + I_D²)

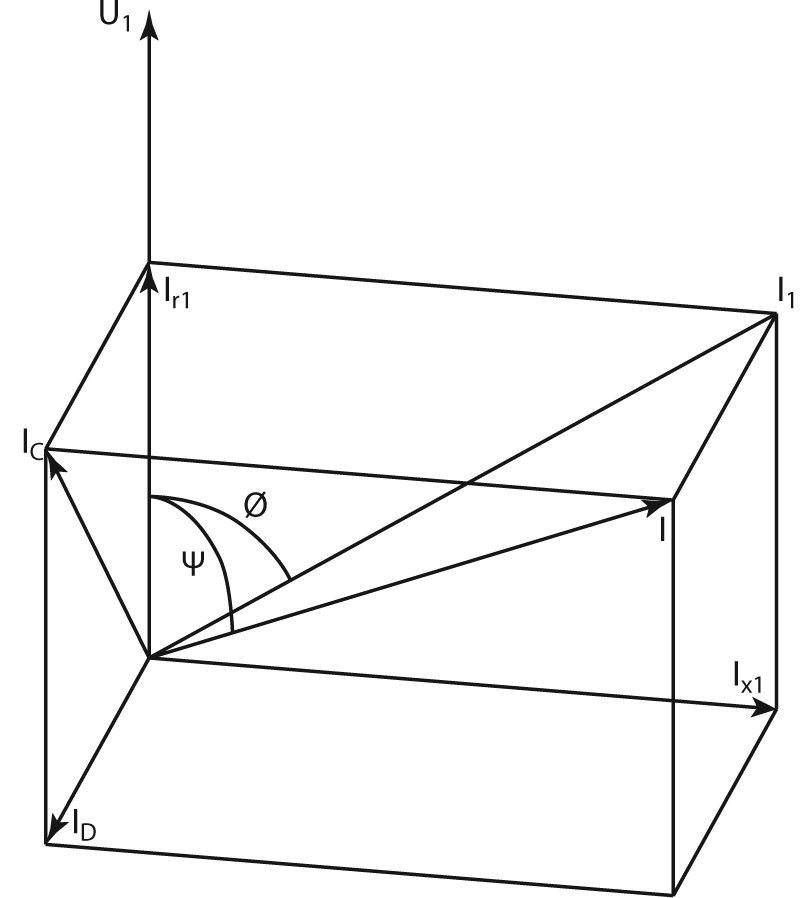
Aquí estamos expresando el verdadero valor eficaz de la corriente total como compuesto por tres componentes: “I_r1”, “I_x1” e “I_D”. Esta ecuación representa al vector “I” como la diagonal de un paralelepípedo rectángulo de lados “I_r1”, “I_x1” e “I_D”. Dicho de otra manera, es el teorema de Pitágoras llevado a tres dimensiones (ver figura 2).
Si, como nos enseña la electrotecnia, ubicamos el vector “U” en la misma línea que “I_r1”, ya que es el componente de la corriente en fase con la tensión, podemos ver que el ángulo entre “U” e “I” (llamado “psi” [ψ] en la gráfica) ahora tiene una ubicación en el espacio de tres dimensiones, a diferencia de lo estudiado clásicamente ubicándolo en un plano de dos dimensiones (ángulo fi [φ] en la gráfica). Esto que expresamos y que da literalmente una nueva dimensión al concepto de potencia aparente (“S = U . I”) es una manera gráfica de mostrar cómo se ha alterado el concepto clásico del plano de potencias con sus componentes activos y reactivos. Se ha agregado ahora una dimensión de componentes de distorsión que nos obliga a otro tipo de análisis. El comportamiento de este nuevo componente de la corriente desde el punto de vista de los efectos producidos en el sistema eléctrico tiene mucha similitud con el componente reactivo. Influye de manera radical cuando llega el momento de estudiar una corrección del factor de potencia. Se observa de la gráfica que no será posible lograr factores de potencia cercanos a la unidad simplemente compensando potencias reactivas mediante capacitores si tenemos una carga fuertemente distorsionada, ya que el componente de distorsión “ID” permanecerá prácticamente inalterado y el valor total de “I” siempre será mayor que “Ir1” y, por lo tanto, si suponemos que “U ≈ U1”, la relación “P/S”, que es el factor de potencia la podemos reducir a:

FP = I₁ . cos φ₁/I

que es igual a decir:

FP = I_r1/I
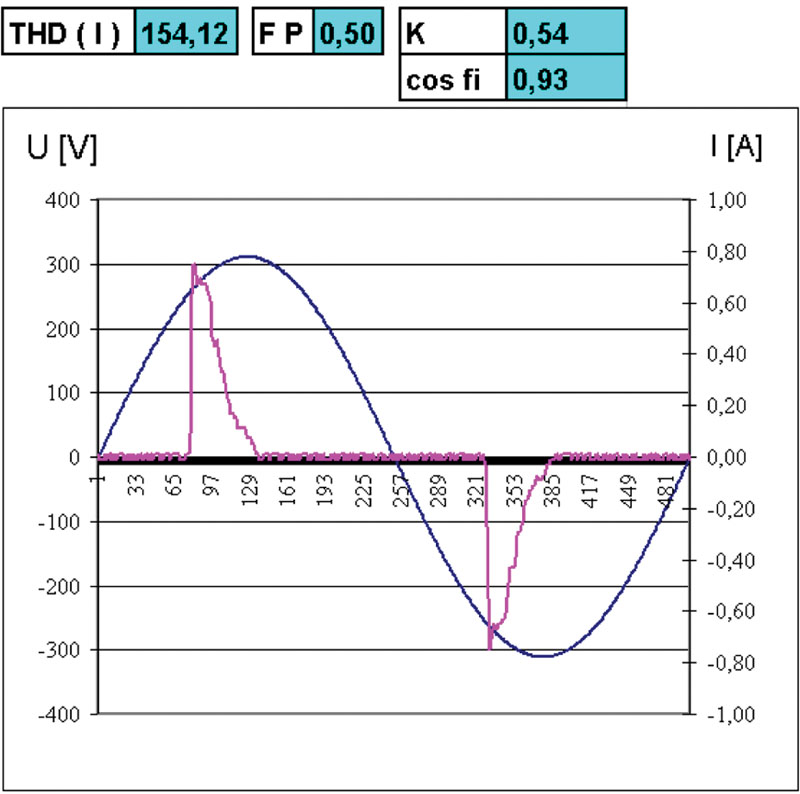
Vamos a ver cada vez con más frecuencia equipamiento que trae especificado su factor de potencia y su coseno de fi como magnitudes separadas.

El método clásico de mejorar el factor de potencia mediante banco de capacitores solo actúa disminuyendo el componente “I_x1”. Si la corriente total tiene un componente de distorsión “I_D” importante, el máximo factor de potencia obtenible, aun compensando completamente la potencia reactiva haciendo “I_x1 = 0”, puede ser bastante menor a uno. Esta situación, con el componente reactivo totalmente compensado dará como resultado la corriente total “Ic”, que podemos ver en la gráfica aún lejos de la posición del vector de tensión “U”, condición necesaria para hacer “S = P” y, por ende, “FP = 1”. Para mejorarlo, estaremos obligados a filtrar los armónicos de la corriente de carga como forma de reducir también la componente “I_D” de la corriente total “I”. Los filtros pasivos permiten reducir el componente reactivo de la corriente fundamental, mejorando “cos φ₁”, y disminuir el componente de armónicos “I_D” de la corriente total, mejorando así el factor de potencia.
Vamos a ver cada vez con más frecuencia equipamiento que trae especificado su factor de potencia y su coseno de fi como magnitudes separadas. Por ejemplo una lámpara del tipo LFC o comúnmente llamada “de bajo consumo”, que trae especificados un coseno de fi del orden de la unidad pero un factor de potencia de 0,50. Esto significa que el componente fundamental de la corriente está en fase con la fundamental de la tensión (cos φ ~ 1) pero su alto contenido de armónicos limita el factor de potencia enormemente (THDi% = 154%).